Building a Binary Adder Using Neural Networks

While taking Andrew Ng’s Machine Learning course, I came across the idea that neurons in neural networks can simulate logic gates. I wanted to prove this by manually building a neural network to perform binary addition, and then later having a neural network learn binary addition via training. This is a really interesting concept: it shows that there is an equivalence between digital circuits and neural networks. The neural network is executing on a digital computer, and it is able to simulate a digital computer. It’s another paradigm of computing, and the mapping I am about to describe is sound and complete. Furthermore, biological neurons perform the same function as artifical neurons, so it also shows an equivalence between digital computers and the brain.

Let’s first take a look at what an individual neuron does:

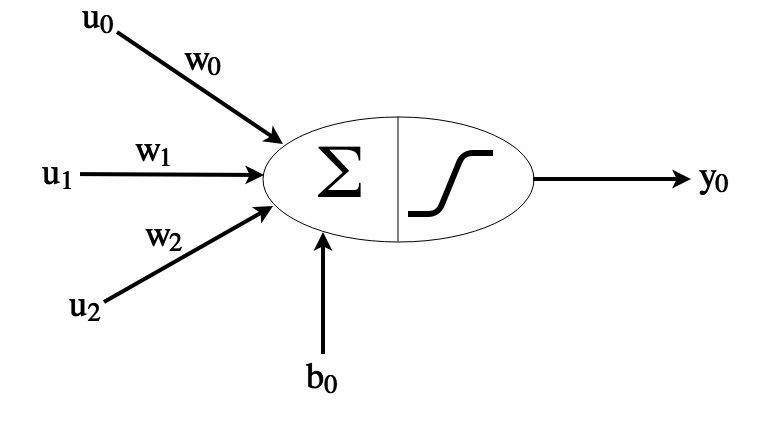
It takes in an array of inputs \(u_0, u_1, u_2\), multiplies each element by its respective weight, and sums this. If the sum is greater than the threshold (\(-b_0\)), output 1, otherwise output 0. Formally, the output is

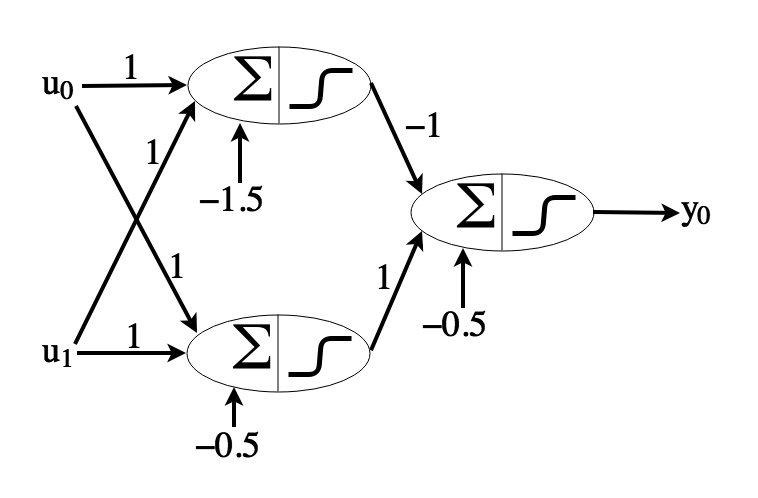
\[y_0 = sigmoid(u_0w_0 + u_1w_1 + u_2w_2 + b_0)\]

where \(sigmoid\) is a smoothed step function outputting 1 if the input is \(> 0\). Using this formula, and restricting the inputs to be 0 or 1, we can build an AND operator:

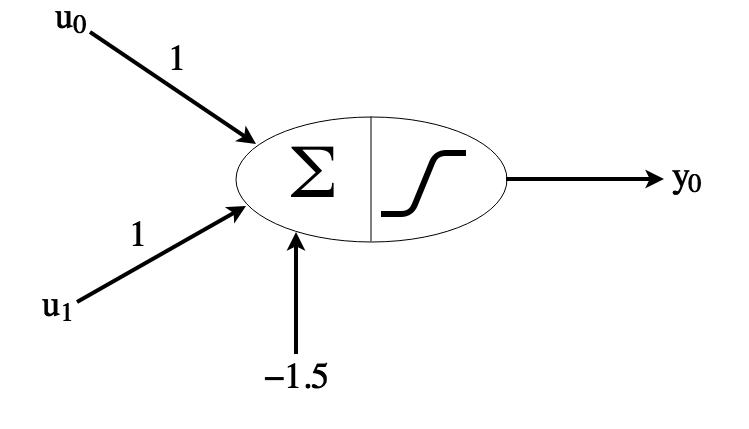
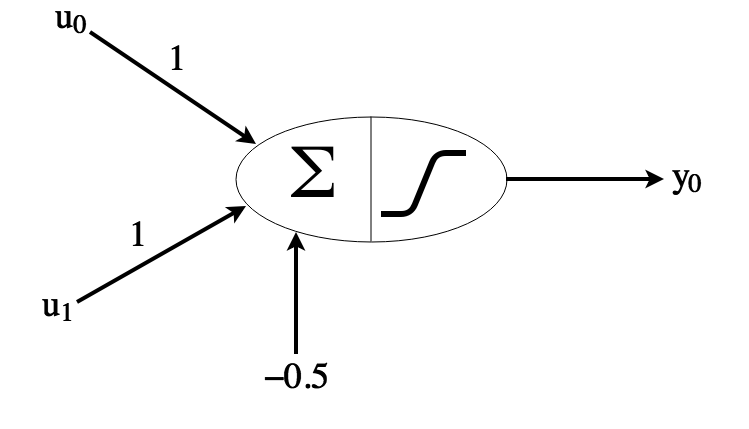
If both inputs are 0, the sum will be -1.5 so the neuron will not activate. If only 1 input is 1, the sum will be -0.5 so the neuron will not activate. If both inputs are 1, the sum will be 0.5 so the neuron will activate. Similarly, we can build an OR operator:

We can also build a NOT operator:

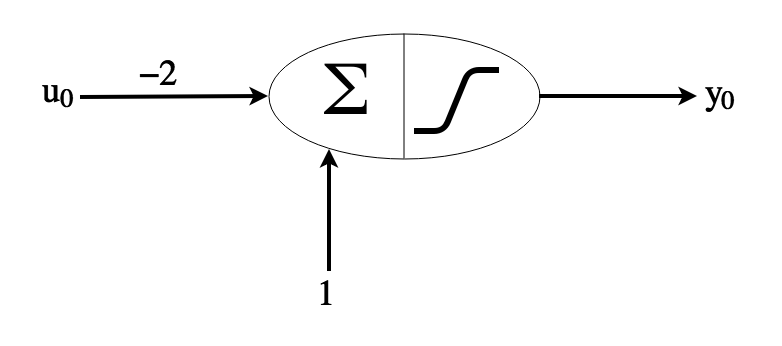
Using these 3 basic logic gates, we can build more complicated gates such as XOR. We can simplify the XOR gate by realizing that \(A\ XOR\ B\) is the same as \((A\ OR\ B)\ AND\ NOT\ (A\ AND\ B)\):

Now that we have the basic conversions from logic gates to neurons, let’s look at the logic circuit for a 2-bit binary adder:

The first output is calculated by XORing the 2 least-significant bits. There is a carry-over only if the first bits are both 1. Translating each logic gate into neurons, the neural network for the binary adder should look like:

This network takes in 4 inputs (2 bits for input a, 2 bits for input b), and outputs 3 bits, since adding 2 bit numbers can result in 3 bits (ex. 3 + 3 = 6, so 11 + 11 = 110). There are 2 hidden layers: the first hidden layer has 6 neurons, and the second hidden layer has 4 neurons. Going from left to right, the layers are of size: 4,6,4,5,3.

We can manually test this network we have built on some inputs and see that it works. Now, let’s use Tensorflow and automatically train a neural network of the same shape to learn binary addition!

We’ll start by importing Tensorflow, and setting the size of the input layer, the 3 intermediate layers, and the output layer:

import tensorflow as tf

input_size = 4
hidden_1_size = 6
hidden_2_size = 4
hidden_3_size = 5
output_size = 3

The Tensorflow python library is mostly just an interface to the main C++ backend which runs in a separate process. In order to communicate with the C++ backend, we need to specify shared data in the form of tf Variables. The input (the 2 2-bit numbers) will be one variable (a vector of size 4), the output will be another (a vector of size 3), and the weights and biases of the network will also be variables. We will specify the weights as matrices.

# Variable to populate with input
x = tf.placeholder("float", [None, input_size])

# Variable which will be populated with output
y = tf.placeholder("float", [None, output_size])

# Variables which we will be learning
weights = {
  'h1': tf.Variable(tf.random_normal([input_size, hidden_1_size])),
  'h2': tf.Variable(tf.random_normal([hidden_1_size, hidden_2_size])),
  'h3': tf.Variable(tf.random_normal([hidden_2_size, hidden_3_size])),
  'out': tf.Variable(tf.random_normal([hidden_3_size, output_size]))
}

biases = {
  'b1': tf.Variable(tf.random_normal([hidden_1_size])),
  'b2': tf.Variable(tf.random_normal([hidden_2_size])),
  'b3': tf.Variable(tf.random_normal([hidden_3_size])),
  'out': tf.Variable(tf.random_normal([output_size]))
}

The rest of the Tensorflow program is left as an exercise to the reader.

Comments